I realize that anyone reading this post doesn’t know what adipra is. How can you? I made it up.
The sphere I constructed most recently was an idea of Karim Adiprasito. While building it, I needed to name it so that I can refer to it in my code. So I temporarily named it adipra and that’s what I’m going to call it here.
Actually, in this post, I don’t want to talk about what adipra is. Not yet. Let’s talk just about what makes adipra special. For anyone who’s interested, all the specifics can be found here.
We need a little language to get started.
Def A combinatorial d-manifold is a triangulated d-manifold whose vertex links are PL spheres.
Let’s assume we know what a triangulated d-manifold means without hashing out the details here. If you need to, you can think of it as a simplicial complex.
The star of a vertex v in a triangulated d-manifold T is the collection of facets of T that contain v. The link of a vertex v is like the star of v, but take out all the v‘s. For example, let’s take a simple hexagon with a vertex in the center.
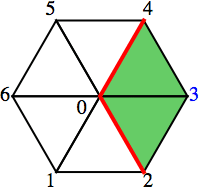
Let T=$\{[0\, 1 \,2],[0\, 1\, 6],[0\, 2\, 3],[0\, 3\, 4],[0\, 4\, 5],[0\, 5\, 6]\}$, then \begin{align*}\text{star}(3,T) &=\{[0\, 2 \,3],[0\, 3\, 4]\} \text{ (green triangles)}\\ \text{link}(3,T)&=\{[0\, 2],[0\, 4]\} \text{ (red edges)} \end{align*}
That’s simple enough to understand even in higher dimensions. Just remember we’re always doing things combinatorially.
Next is the PL sphere. I said earlier that we can assume we know what a triangulated d-manifold is. What we’re actually talking about is a triangulated PL d-manifold. A PL-sphere is a PL manifold that is bistellarly equivalent to the boundary of a d-simplex. I’ll write in more detail what bistellarly equivalent means in a later post. For now, just think of it as the discrete version of being homeomorphic.
Putting all that together, we understand a combinatorial d-manifold to be a triangulated manifold, that is, some simplicial complex-like thing where we require that each of its verticies is sort of covered by a ball. Naturally, the next question to ask is: are there triangulated manifolds that are not combinatorial?
For d=2,3, all triangulations (of the d-sphere) are combinatorial. For d=2, the vertex links should be homeomorphic to $S^1$ or bistellarly equivalent to the triangle (boundary of a 2-simplex). Similarly, for d=3, vertex links are $S^2$. For d=4, all triangulated 4-manifolds are also combinatorial. This result is due to Perelman. The vertex links are 3-spheres, which, as you know, is what Perelman worked on. [Remember that PL=DIFF in dim 4.] But it falls apart for d$\ge 5$ as there are non-PL triangulations of the d-sphere.
Ok, so here’s a spoiler about adipra: it’s a non-PL triangulation of the 5-sphere. But that’s not all.
There’s a nice theorem by Robin Forman, the father of discrete Morse theory.
Theorem (Forman) Every combinatorial d-manifold that admits a discrete Morse function with exactly two critical cells is a combinatorial d-sphere.
Actually, this is not really Forman’s theorem. This is a theorem by Whitehead which Forman reformulated using his language of discrete Morse theory. This is the original theorem.
Theorem (Whitehead) Any collapsible combinatorial d-manifold is a combinatorial d-ball.
What Forman did is take a sphere, take out one cell, call that guy a critical cell, then collapse the rest of it down (using Whitehead’s theorem) to get the other critical cell. Thus you have two critical cells.
So the question you ask next is: can you have non-combinatorial spheres with 2 critical cells?
Yes, actually, you can! Karim showed that you can have a non-PL/non-combinatorial triangulation of the 5-sphere that has a discrete Morse function with exactly 2 critical cells! And then I built an explicit example (with Karim’s instructions) and called it adipra.