Category: spheres

Constructing complicated spheres

The significance of adipra

/ matsguru

I realize that anyone reading this post doesn’t know what adipra is. How can you? I made it up.

The sphere I constructed most recently was an idea of Karim Adiprasito. While building it, I needed to name it so that I can refer to it in my code. So I temporarily named it adipra and that’s what I’m going to call it here.

Actually, in this post, I don’t want to talk about what adipra is. Not yet. Let’s talk just about what makes adipra special. For anyone who’s interested, all the specifics can be found here.

We need a little language to get started.

Def A combinatorial d-manifold is a triangulated d-manifold whose vertex links are PL spheres.

Let’s assume we know what a triangulated d-manifold means without hashing out the details here. If you need to, you can think of it as a simplicial complex.

The star of a vertex v in a triangulated d-manifold T is the collection of facets of T that contain v. The link of a vertex v is like the star of v, but take out all the v‘s. For example, let’s take a simple hexagon with a vertex in the center.

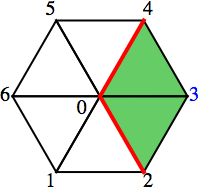
vertexlink
Example of star and link of vertex

Let T=$\{[0\, 1 \,2],[0\, 1\, 6],[0\, 2\, 3],[0\, 3\, 4],[0\, 4\, 5],[0\, 5\, 6]\}$, then \begin{align*}\text{star}(3,T) &=\{[0\, 2 \,3],[0\, 3\, 4]\} \text{ (green triangles)}\\ \text{link}(3,T)&=\{[0\, 2],[0\, 4]\} \text{ (red edges)} \end{align*}

That’s simple enough to understand even in higher dimensions. Just remember we’re always doing things combinatorially.

Next is the PL sphere. I said earlier that we can assume we know what a triangulated d-manifold is. What we’re actually talking about is a triangulated PL d-manifold. A PL-sphere is a PL manifold that is bistellarly equivalent to the boundary of a d-simplex. I’ll write in more detail what bistellarly equivalent means in a later post. For now, just think of it as the discrete version of being homeomorphic.

Putting all that together, we understand a combinatorial d-manifold to be a triangulated manifold, that is, some simplicial complex-like thing where we require that each of its verticies is sort of covered by a ball. Naturally, the next question to ask is: are there triangulated manifolds that are not combinatorial?

For d=2,3, all triangulations (of the d-sphere) are combinatorial. For d=2, the vertex links should be homeomorphic to $S^1$ or bistellarly equivalent to the triangle (boundary of a 2-simplex). Similarly, for d=3, vertex links are $S^2$. For d=4, all triangulated 4-manifolds are also combinatorial. This result is due to Perelman. The vertex links are 3-spheres, which, as you know, is what Perelman worked on. [Remember that PL=DIFF in dim 4.] But it falls apart for d$\ge 5$ as there are non-PL triangulations of the d-sphere.

Ok, so here’s a spoiler about adipra: it’s a non-PL triangulation of the 5-sphere. But that’s not all.

There’s a nice theorem by Robin Forman, the father of discrete Morse theory.

Theorem (Forman) Every combinatorial d-manifold that admits a discrete Morse function with exactly two critical cells is a combinatorial d-sphere.

Actually, this is not really Forman’s theorem. This is a theorem by Whitehead which Forman reformulated using his language of discrete Morse theory. This is the original theorem.

Theorem (Whitehead) Any collapsible combinatorial d-manifold is a combinatorial d-ball.

What Forman did is take a sphere, take out one cell, call that guy a critical cell, then collapse the rest of it down (using Whitehead’s theorem) to get the other critical cell. Thus you have two critical cells.

So the question you ask next is: can you have non-combinatorial spheres with 2 critical cells?

Yes, actually, you can! Karim showed that you can have a non-PL/non-combinatorial triangulation of the 5-sphere that has a discrete Morse function with exactly 2 critical cells! And then I built an explicit example (with Karim’s instructions) and called it adipra.

KolKom 2012

/ matsguru / 1 Comment

My first conference talk since starting Phase II was at KolKom 2012, the colloquium on combinatorics in Berlin. But I don’t know anything about combinatorics or optimization. What am I doing at a combinatorics conference!?

Actually, I don’t know much about anything. But it’s not hard to make me sound like I know about some things. The title of my talk was “constructing complicated spheres as test examples for homology algorithms”. Yes, algorithms! That’s the key! It was Frank’s idea to add the word “algorithms” to my title so that I can at least pretend to belong to this conference. It made for a very long title, but at least my abstract was accepted.

You can look at my slides, but I’ll give a short overview here.

We begin with a definition of homology and motivate some applications for homology algorithms. Betti numbers, in particular, are interesting for industrial applications. To compute the Betti numbers of some given simplicial complex, we will be dealing with matrices. We want to find the Smith Normal Form of these matrices. But the bigger the complex, the bigger the matrix, and the longer it takes to find the Smith normal form. So we throw the complex into a preprocess to reduce the size of the input. This preprocess uses discrete Morse theory.

Morse theory is used to distinguish topological spaces in differential topology. Forman came up with a nice discrete counterpart that conveniently preserves many of the main results from smooth Morse theory including the Morse inequalities. The Morse inequality $\beta_i \le c_i \; \forall i$ means that the Betti number $\beta_i$ is bounded above by $c_i$, the number of critical points of dimension $i$. Since our original goal was to compute Betti numbers, this result will definitely come in handy.

The critical points $c_i$ are the critical points of some discrete Morse function. These discrete Morse functions can be interpreted as a sort of collapse. By collapsing big complexes, we can reduce big complexes (that have big matrices for which we need to find the Smith normal form) to smaller complexes.

Ideally, we want to find the discrete Morse function with the lowest $c_i$’s. But computing the optimal discrete Morse vector, a vector $c = (c_0,c_1,c_2, \dots)$, is $\mathcal{NP}$-hard! So Lutz and Benedetti have come up with the idea of using random discrete Morse theory. Surprisingly, their algorithm is able to find the optimal discrete Morse vector most (but not all) of the time. To get a better idea of when they’re better able to find the optimum, they came up with a complicatedness factor which measures how hard it is to find that optimum.

That’s where I come in. I constructed some complicated simplicial complexes. They are being used to test some homology algorithms that are currently under development.

The first of my complicated complexes is the Akbulut-Kirby sphere, one of a family of Cappell-Shaneson spheres. These spheres have an interesting history. The AK-sphere, in particular, was one thought to be an exotic sphere. Exotic spheres are spheres that are homeomorphic, but not diffeomorphic to a standard sphere. In dimension $4$, this would mean it could be a counterexample to the smooth Poincar\’e conjecture, or SPC4 for short. Unfortunately, some years after the AK-sphere was proposed, it was shown to be standard after all. You can learn more about it here.

So I built an AK-sphere. Actually, I wrote code that can build any of the whole family of the CS-spheres. Before talking about what we did, let’s start with how these spheres are built. To understand the construction, you have to first accept two simple ideas:

  • The boundary of a solid ball is a sphere.
That’s not too hard to accept, which is why I said it first even though it’s the last step.
  • Given a donut, if you fill the “hole” (to make it whole, HA!), it will become a solid ball.

That’s also not too difficult to see. You can imagine the filling to be something like a solid cylinder that you “glue” onto the inside part of the donut.

Now for some language. This donut is actually a ball with a handle, which is known as a 1-handle. The filling for the hole is called a 2-handle. And we can specify how the 2-handle is glued in using an attaching map.

So to build the AK-sphere here’s what we do:

  1. Take a 5-ball.
  2. Attach two 1-handles. Let’s call one of them $x$ and the other $y$ so we can tell them apart.
  3. Glue in two 2-handles to close the “holes” but use attaching maps that have the following presentation: \begin{align*} xyx&= yxy & x^r = y^{r-1}\end{align*}This means that the attaching map goes (on the boundary of the 5-ball) along $x$ first, then $y$, then $x$, then $y$ in the reverse direction, then $x$ in reverse, and finally $y$ in reverse. Similarly with $x^r = y^{r-1}$. [Note: For the AK-sphere, $r = 5$. By varying $r$ you get the family of CS-spheres.]
  4. Take its boundary.

Since the 2-handles have closed the holes created by the 1-handles, what we have left after step 3 is again a 5-ball, though a bit twisted. So its boundary in step 4 should be a sphere.

To construct these spheres, we decided to go in a different order. It would be hard to imagine the attaching maps in dimension 5. So we went down a smidge to dimension 3. And instead of drawing the paths of the attaching maps on/in a ball, we built the ball around the paths.

As you might imagine, these paths come out a bit knotted. But by bringing them up in dimension, we can “untangle” it because there’s more space in higher dimensions. The way that we go up in dimension is by “crossing by $I$” where $I$ is the usual unit interval. Crossing by $I$ has the convenient side effect that everything you “crossed” ends up on the boundary of the resulting complex.

So we start with these two paths (some triangulated torii). We fill in the space between them with cleverly placed tetrahedra so that it ends up being a ball with two 1-handles. We now have a genus 2 simplicial complex, where two sets of tetrahedra are labelled as the path representing $xyx = yxy$ and the other $x^r = x^{r-1}$. Cross $I$, cross $I$ so that we are in dimension 5 with the two paths on the boundary of this ball with two 1-handles. Glue in the (5-dimensional) 2-handles (whatever that means). Take the boundary. Done!

The experiments we’ve run on them so far have shown some promise. The complexes are not too large (with f-vector$=(496,7990,27020,32540,13016)$) so the experiments don’t take too long to run. They’ve already been used by Konstantin Mischaikow and Vidit Nanda to improve their on-going Perseus algorithm. [edit: In the original post, I mistakenly referenced CHomP, which has been static for some time.]

The other complex I constructed is Mazur’s 4- manifold. We do a similar thing, but this time there’s only one path to deal with (that is, only one 1-handle to close up with one 2-handle). The results from this one has some nice topological properties. I’ll get to that in a later post once we’re ready to publish.