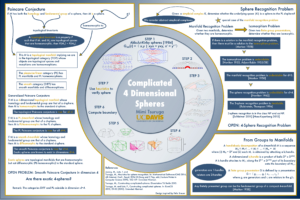
Our triangulations of the Akbulut-Kirby Spheres
Manifold recognition is known to be unsolvable for dimensions [latex]d \ge 4[/latex] [Markov]. The related sphere recognition problem is known to be undecidable for dimensions [latex]d > 4[/latex]. However, 3-sphere recognition is decidable [Rubinstein, Thompson], but was found to be NP [Schleimer] and co-NP [Hass-Kuperberg]. The decidability of the 4-sphere recognition problem is still unknown.
Fortunately, there are several heuristic methods which can effectively and quickly recognize spheres to be spheres for all triangulations (or, more accurately, simplicial complexes) that we know of. Except, that is, for the family of examples which we constructed: our triangulations of the Akbulut-Kirby spheres.
The Akbulut-Kirby spheres were originally introduced as candidate exotic spheres [Akbulut-Kirby]. Selman Akbulut and Rob Kirby described a smooth manifold which is homeomorphic to a 4-dimensional sphere, but could not find a diffeomorphism to the sphere. If they could prove that there are no diffeomorphisms to the sphere, then they would have found a counterexample to the smooth Poincare conjecture in dimension 4. It took over 2 decades, but Akbulut himself found that diffeomorphism [Akbulut]. And the smooth Poincare conjecture in dimension 4 is still an open problem today.
Akbulut and Kirby simplified the description enough that one can follow the general idea without being an expert in differential topology and Kirby calculus.
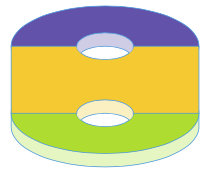
Start with a 4-dimensional ball to which we attach two handles (like the handle on a coffee mug). Formally these handles are called one-handles. So we have now attached two one-handles. We then label each handle so we can keep track of which is which. Let us call the purple one [latex]x[/latex] and the green one [latex]y[/latex]. Notice the image is a 3-dimensional depiction of our 4-manifold.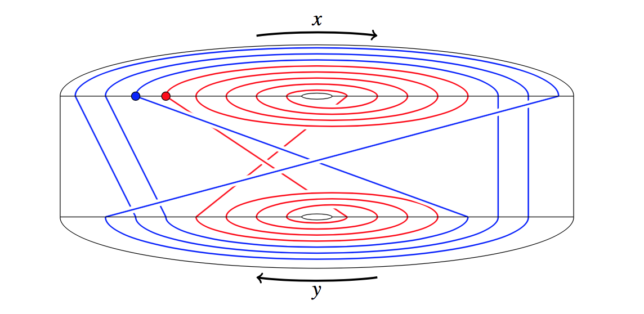 We then want to glue two 4-balls onto this manifold to close up the two holes that we introduced when we attached the two one-handles in the beginning. But we will glue them on in a non-trivial way. We will follow along the two paths (red and blue) shown above. If you start from the blue dot and walk along, you’ll find the blue path goes along the [latex]x[/latex]-handle, then [latex]y[/latex], then [latex]x[/latex], then the [latex]y[/latex]-handle backwards, then [latex]x[/latex] backwards, then [latex]y[/latex] backwards, and return to the blue dot. We describe this blue path as [latex]xyxy^{-1}x^{-1}y^{-1}[/latex] and the red one is [latex]x^5y^{-4}[/latex].
We then want to glue two 4-balls onto this manifold to close up the two holes that we introduced when we attached the two one-handles in the beginning. But we will glue them on in a non-trivial way. We will follow along the two paths (red and blue) shown above. If you start from the blue dot and walk along, you’ll find the blue path goes along the [latex]x[/latex]-handle, then [latex]y[/latex], then [latex]x[/latex], then the [latex]y[/latex]-handle backwards, then [latex]x[/latex] backwards, then [latex]y[/latex] backwards, and return to the blue dot. We describe this blue path as [latex]xyxy^{-1}x^{-1}y^{-1}[/latex] and the red one is [latex]x^5y^{-4}[/latex].
We started with a 4-ball, introduced two holes, then closed off those holes. So we’re back to having just a ball. Make a copy of that ball. Then match up the boundaries of the two balls. And voila: we get a 4-dimensional sphere.
This sphere we constructed is described by the finitely presented group [latex]G = \langle x,y \mid xyx=yxy. x^5 = y^4 \rangle[/latex], which you can read all about in the beginning of Kirby’s Topology of 4-manifolds.
That’s essentially the entire construction.
We developed a few simplicial versions of this procedure. It was a bit involved (enough for me to get a PhD), but we produced some nice pictures. Here’s a taste. For more details, check out the dissertation or the preprint.
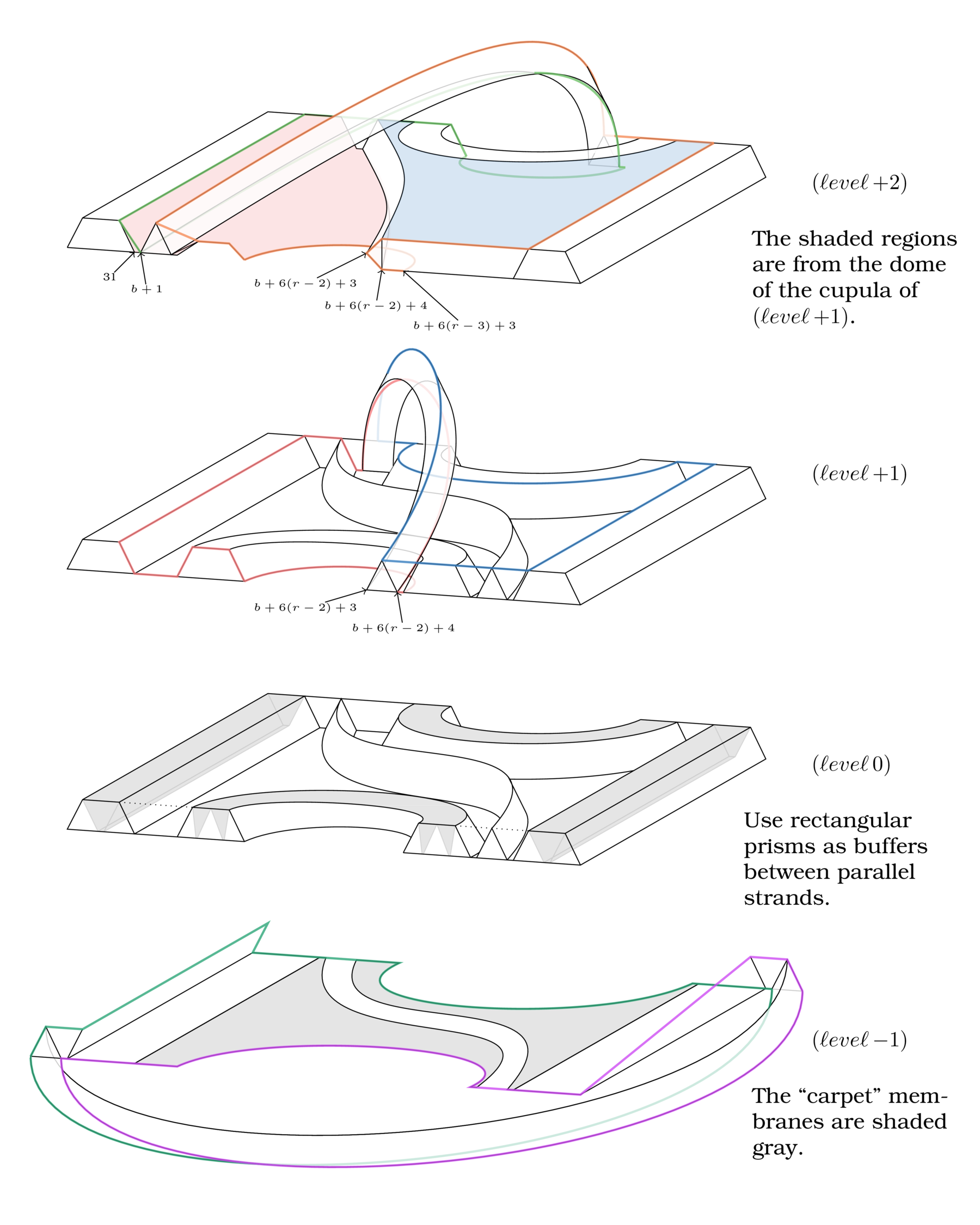
We know that the manifolds we constructed are proper 4-spheres by Akbulut’s proof and the fact that in dimension 4, PL=DIFF. Yet, none of the sphere recognition heuristic software we know of have been able to correctly recognize them to be spheres. To our knowledge, these are the only such examples.
For a more graphical summary of this project, check out this poster that was presented at the MSRI Modern Math Workshop at SACNAS 2015.
References
- S Akbulut. Cappell–Shaneson homotopy spheres are standard. Ann. Math., 171:2171–2175, 2010
- S Akbulut and R Kirby. A potential smooth counterexample in dimension 4 to the Poincaré conjecture, the Schoenflies conjecture, and the Andrews– Curtis conjecture. Topology, 24:375–390, 1985.
- J Hass and G Kuperberg. The complexity of recognizing the 3-sphere. Oberwolfach Reports, 24:1425–1426, 2012.
- A Markov. The insolubility of the problem of homeomorphy. Dokl. Akad. Nauk SSSR, 121:218–220, 1958.
- JH Rubinstein. An algorithm to recognize the 3-sphere. In S. D. Chatterji, editor, Proc. Internat. Congr. of Mathematicians, ICM ’94, Zürich, Volume 1, pages 601–611, Basel, 1995. Birkhäuser Verlag.
- S Schleimer. Sphere recognition lies in NP. In Low-dimensional and symplectic topology, volume 82 of Proc. Sympos. Pure Math., pages 183– 213. Amer. Math. Soc., Providence, RI, 2011.
- A Thompson. Thin position and the recognition problem for [latex]S^3[/latex]. Math. Res. Lett., 1(5):613–630, 1994.